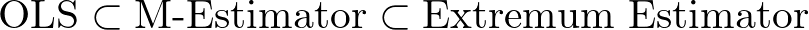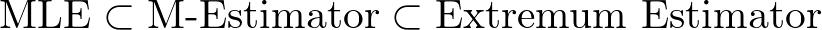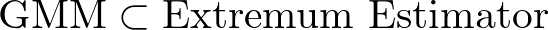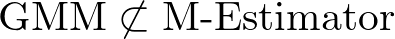計量経済学や統計学を学んでいると、OLS、MLE、GMM など様々な推定量が登場します。
これらを個別に覚えたり一致性を導出したりするのは大変ですが、実はこれらはすべて「極値推定量(Extremum Estimator)」という一つの大きなフレームワークに含まれます。
この記事では、Extremum Estimator の全体像と、混同しやすい「M推定量」との違い、そして各手法がどのように対応しているのかをスッキリ整理します。
大学院のコア計量2で登場する内容です!

Contents
極値推定量とM推定量の違い
まず、もっとも大きな枠組みが極値推定量(Extremum Estimator)です。
極値推定量とは?
データに基づいて定義される「目的関数 \( Q_{n}(\theta) \) 」を最小化(または最大化)することで得られる推定量の総称です。
\[ \hat{\theta} = \arg\min_{\theta\in\Theta} Q_{n}(\theta) \]
目的関数にマイナスをつけてやれば最小化問題は最大化問題になるので、最小化であろうと最大化であろうと、どちらも本質的には一緒です。
本記事では、「最小化」で統一します。
\( Q_{n} \) はデータから計算される目的関数
上記にも書いてある通り、\( Q_{n} \) はデータから計算される目的関数であり(だからこそサンプルサイズ \( n \) に依存する)、それを最小化することで推定量 \( \hat{\theta} \) が求まります:
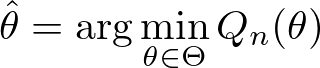
すなわち、\( Q_{n} \) はサンプルの関数だと言えます。
\( Q \) は母集団の目的関数
これに対し、Extremum Estimator では母集団の目的関数も考えます。これを \( Q \) とします。
この \( Q \) は \( n \) に依存しません。
そして、我々が推定したい真のパラメーター \( \theta_{0} \) は、この \( Q \) を最小化します:
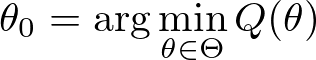
すなわち、\( Q \) は population の目的関数です。
そして、その sample に対応するもの(sample counterpart)が \( Q_{n} \) です。
M推定量との違い
以上が、極値推定量(Extremum Estimator)のフレームワークでした。それでは、M推定量について見ていきましょう。
M推定量(M-estimator)は、極値推定量 (Extremum Estimator) の一種です。すなわち、
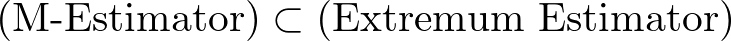
M推定量の最大の特徴は、目的関数がサンプル平均(各データの和)の形をしていることです。
- 極値推定量: 目的関数 \( Q_{n} \) の形に制限なし(広い)
- M推定量: 目的関数 \( Q_{n} \) が \( \sum_{i=1}^{n} q(w_{i},\theta) \) という「和」の形(狭い)
重要なのは、
ポイント
M推定量は Extremum Estimator の一部!
OLS, MLE, GMM はなぜ Extremum Estimator なのか?
これらの手法はすべて、「何かを最小(最大)にする」というプロセスを経るため、極値推定量の定義に当てはまります。
それぞれの目的関数を見てみましょう。
① 最小二乗法 (OLS)
Extremum Estimator の1つ目の例は、OLS です。
OLS は、残差平方和を最小化します。
例1:OLS
OLS は、実際の値と予測値の残差平方和(RSS)を最小化する手法です。
- 目的関数: \( Q_{n}(\beta) = \sum_{i=1}^{n} (y_{i}-x_{i}^{\prime} \beta)^{2} \)
- 極値操作: この \( Q_{n}(\beta) \) を 最小化(Minimize) する \( {\beta} \) を探し、 \( \hat{\beta} \) とします。
データから計算される \( Q_{n} \) は上記のように求まります。これは OLS 推定量の定義そのものですね。
それでは、母集団の \( Q \) はどのように定式化されるでしょうか。
例1:OLS(続き)
OLS の母集団における目的関数とパラメーターは以下のようになります。
- 目的関数: \( Q(\beta) = E\left[ (y-x^{\prime} \beta)^{2} \right] \)
- 真のパラメーター: この \( Q(\beta) \) を 最小化(Minimize) する \( {\beta} \) が、真のパラメーター \( {\beta}_{0} \) です。
真のパラメーター \( \beta_{0} \) が母集団の \( Q \) を最小化することを式で見てみましょう。
真のパラメーター \( \beta_{0} \) が母集団の \( Q \) を最小化することの証明はこちらをクリック
\( Q (\beta) = E\left[ (y-x^{\prime} \beta)^{2} \right] \) は \( \beta \) に関して凸ですから、FOC が必要十分条件です。なお、ここでは微分と積分の交換を許します。
\begin{align}
0 = \frac{\partial}{\partial\beta} Q(\beta)
&= E\left[ \frac{\partial}{\partial\beta} (y-x^{\prime} \beta)^{2} \right] \\
&= E\left[ -2x(y-x^{\prime}\beta) \right]
\end{align}より \[ E\left[ xy - xx^{\prime}\beta_{0} \right] = 0 \] を得ます。よって、\[ \beta_{0} = E[xx^{\prime}]^{-1} E[xy] \] です。これはとりもなおさず OLS における真のパラメーターです。(証明終)
② 最尤法 (MLE)
Extremum Estimator の2つ目の例は、MLE です。
MLE は、尤度関数(または対数尤度関数)を最大化します。
例2:MLE
MLE は、手元のデータが得られる確率(尤度)が最も高くなるようなパラメータを推定する手法です。通常は計算を楽にするために対数をとります。
- 目的関数: \( Q_{n}(\theta) = -\sum_{i=1}^{n} \log f(y_{i}\mid x_{i};\theta) \)(対数尤度関数)
- 極値操作: この \( Q_{n}(\theta) \) を 最小化(Minimize)(=対数尤度を最大化) する \( \theta \) を探し、 \( \hat{\theta} \) とします。
それでは、母集団の方を見てみましょう。
例2:MLE(続き)
MLE の母集団における目的関数とパラメーターは以下のようになります。
- 目的関数: \( Q(\theta) = -E\left[ \log f(y\mid x;\theta) \right] \)
- 真のパラメーター: この \( Q(\theta) \) を 最小化(Minimize) する \( {\theta} \) が、真のパラメーター \( {\theta}_{0} \) です。
真のパラメーター \( \theta_{0} \) が \( Q(\theta) \) を最小化することの証明はこちらをクリック
まず、設定を確認しておきます。密度関数が \( f(y\mid x;\theta) \) であり、真のパラメーターが \( \theta_{0} \) です。
次に、任意に \( \theta\in\Theta \) をとり固定し、以下のものを評価します:
&\ E\left[ \log \left( \frac{ f(y\mid x;\theta) }{ f(y\mid x; \theta_{0}) } \right) \right] \\
&\stackrel{\text{LIE}}{=} E\left\{ E\left[ \log \left( \frac{ f(y\mid x;\theta) }{ f(y\mid x; \theta_{0}) } \right) \mid x \right] \right\} \\
&\stackrel{\text{Jensen}}{\le} E\left\{ \log \left( E \left[ \frac{ f(y\mid x;\theta) }{ f(y\mid x; \theta_{0}) } \mid x \right] \right) \right\} \quad \cdots \text{(A)}
\end{align}
\begin{align}
&\ E\left\{ \log \left( E \left[ \frac{ f(y\mid x;\theta) }{ f(y\mid x; \theta_{0}) } \mid x \right] \right) \right\} \\
&= E\left\{ \log \left( \int \frac{ f(y\mid x;\theta) }{ f(y\mid x; \theta_{0}) } \cdot f(y\mid x; \theta_{0}) dy \right) \right\} \\
&= E\left\{ \log \left( \int f(y\mid x;\theta) dy \right) \right\} \quad \cdots \text{(B)}
\end{align} となります。ここで、\( f(y\mid x;\theta) \) は密度関数ですから、積分すると 1 になります:\begin{align}
&\ E\left\{ \log \left( \int f(y\mid x;\theta) dy \right) \right\} \\
&= E[\log (1)] \\
&= E[0] \\
&= 0 \quad \cdots \text{(C)}
\end{align} (A),(B),(C) により、\[ E\left[ \log \left( \frac{ f(y\mid x;\theta) }{ f(y\mid x; \theta_{0}) } \right) \right] \le 0 \] が従います。すなわち、\[ E\left[ \log f(y\mid x;\theta) - \log f(y\mid x;\theta_{0}) \right] \le 0 \] \[ E\left[ \log f(y\mid x;\theta) \right] \le E\left[ \log f(y\mid x;\theta_{0}) \right] \] です。
\( \theta\in\Theta\) は任意でしたから、\( \theta_{0} \) が \( E\left[ \log f(y\mid x;\theta) \right] \) を最大化することがわかります。ゆえに、\( \theta_{0} \) はマイナスのついた目的関数 \( Q(\theta) = -E\left[ \log f(y\mid x;\theta) \right] \) を最小化します。(証明終)
③ 一般化積率法 (GMM)
Extremum Estimator の3つ目の例は、GMM です。
GMM は、積率条件(モーメント条件)がゼロに近づくように、二次形式の距離関数を最小化します。
例3:GMM
GMM は、「母集団での期待値がゼロになる」というモーメント条件をサンプルで近似し、そのズレ(距離)を最小化する手法です。
- 目的関数: \( Q_{n}(\theta) = g_{n}(\theta)^{\prime}W_{n} g_{n}(\theta) \)
- \( g_{n}(\theta) \) はサンプルモーメント、\( W_{n} \) は重み行列です。
- 極値操作: この \( Q_{n}(\theta) \) を 最小化(Minimize) する \( \theta \) を探し、 \( \hat{\theta} \) とします。
それでは、母集団に対応するものを見てみましょう。
GMM において真のパラメーター \( \theta_{0} \) は以下を満たすものとして定義されます:
\[ E\left[ g(w,\theta) \right] = 0 \quad \text{iff} \quad \theta = \theta_{0} \]
すなわち、\( \theta=\theta_{0} \) のとき、およびそのときのみ、モーメント等式 \( E\left[ g(w,\theta) \right] = 0 \) が満たされます。
例3:GMM(続き)
GMM の母集団における目的関数とパラメーターは以下のようになります。
- 目的関数: \( Q(\theta) = E[ g(w,\theta) ]^{\prime} W E\left[ g(w,\theta) \right] \)
- \( g(w,\theta) \) はモーメント条件の中身の関数、\( W \) は母集団における重み行列です。\( W \) は正定値(positive definite)であるとします。
- 真のパラメーター: この \( Q(\theta) \) を 最小化(Minimize) する \( {\theta} \) が、真のパラメーター \( {\theta}_{0} \) です。
\( \theta=\theta_{0} \) のとき、およびそのときのみ、モーメント等式 \( E\left[ g(w,\theta) \right] = 0 \) が満たされるわけですから、\( \theta \ne \theta_{0} \) のときは
\[ Q(\theta) = E[ g(w,\theta) ]^{\prime} W E\left[ g(w,\theta) \right] > 0 \]
となります(\( W \) は正定値のため)。
一方、\( \theta=\theta_{0} \) のときはモーメント等式 \( E\left[ g(w,\theta_{0}) \right] = 0 \) が満たされ、
\[ Q(\theta_{0}) = E[ g(w,\theta_{0}) ]^{\prime} W E\left[ g(w,\theta_{0}) \right] = 0 \]
となります。したがって、\( \theta_{0} \) は \( Q (\theta) \) の最小解です。
なお、この \( g(w_{i},\theta) \) という notation を使うと、サンプルモーメント \( g_{n}(\theta) \) は
\[ g_{n}(\theta) = \frac{1}{n}\sum_{i=1}^{n} g(w_{i},\theta) \]
と書けます。
なぜ GMM は「M推定量」ではないのか?
ここが混乱しやすいポイントです。
OLS と MLE は M推定量だが、
GMM は M推定量ではない
という点です。
OLS と MLE が M推定量である理由
上の式を見ればわかる通り、OLSもMLEも
∑ (各データごとの関数)
という形をしています。
つまり、1つ1つのデータが独立に目的関数に寄与しており、シンプルに足し算されているため、M推定量の定義に合致するのです。
GMM が M推定量ではない理由
GMM の目的関数をもう一度見てみましょう。
この式は「和をとった後のものを、さらに外側で掛け合わせている(二次形式)」構造になっています。
これを \[ Q_{n}(\theta) = \sum_{i=1}^{n} q(w_{i},\theta) \] という「一つの和」の形に書き直すことはできません。
このように、GMM はデータ全体の平均を操作してから二乗するような構造を持つため、
GMM は極値推定量ではあっても、M推定量(単純な和の形)ではないのです。
まとめ
最後に、この記事の内容をテーブルとイメージでまとめます。
| 手法 | Extremum Estimator? | M推定量? | 目的関数の特徴 |
| OLS | ✅ | ✅ | 残差平方の和 |
| MLE | ✅ | ✅ | 対数尤度の和 |
| GMM | ✅ | ❌ | モーメントの平均の二次形式 |