【時系列解析】コクラン・オーカット法の仕組み

コクラン・オーカット法（Cochrane-Orcutt estimation）は、計量経済学や統計学において、回帰分析の「系列相関（自己相関, serial correlation）」を解決するための手法です。

時系列データで最小二乗法（OLS）を用いると、誤差項同士に相関（昨日と今日の誤差が似ているなど）が生じることがあります。

これがあると、OLSによる推定は「効率的」ではなくなり、標準誤差の計算が狂って正しい検定ができなくなります。コクラン・オーカット法はこの問題をデータを変換することで解決します。

コクラン・オーカット法の仕組み

この手法は、以下のAR(1)モデル（1期前の誤差に依存するモデル）を前提としています。

1. 元のモデル: \( y_{t} = \alpha + \beta x_{t} + e_{t},\qquad t=1,\ldots,T \)
2. 誤差項の相関: \( e_{t} ​= \rho e_{t−1} ​+ u_{t}​,\qquad |\rho|<1 \) （\( u_{t} \)​ はホワイトノイズ）

まずは簡単のために \(\rho\) が既知 (known) であるとして話を進めます。

また、\(u_{t}\) がホワイトノイズであるとは、(i) mean zero (\(E[u_{t}]=0\)) (ii) homoskedastic (\( \mathrm{Var}(u_{t}) = \sigma^{2} \) で一定) (iii) serially uncorrelated (\( \mathrm{Cov}(u_{i},u_{j}) = 0,\ \forall i\ne j \)) を満たすときにいいます。

この \(\rho\)（自己相関係数）の影響を取り除くために、データを以下のように準差分変換します。

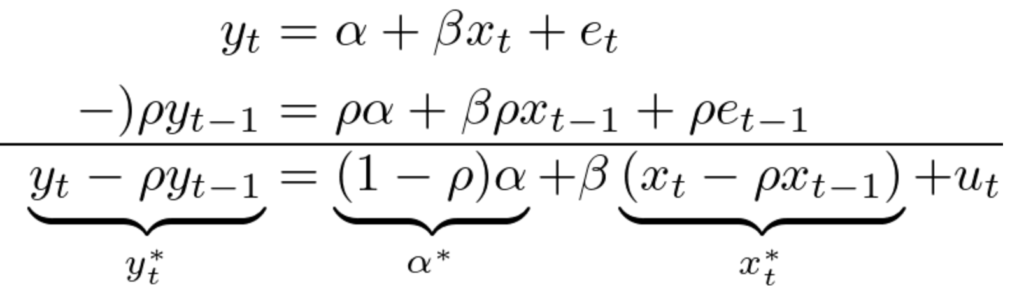
このようにすれば、

• \( y_{t}^{*} = y_{t} - \rho y_{t-1} \) を
• \( x_{t}^{*} = x_{t} - \rho x_{t-1} \) と定数項に OLS 回帰

することによって、係数 \(\beta\) が求まります。

\(\rho\) が既知であるため、\( y_{t}^{*} = y_{t} - \rho y_{t-1} \) も既知となり、この回帰を回すことができます（\( x_{t}^{*} = x_{t} - \rho x_{t-1} \) についても同様）。

このとき、OLS 推定は効率的です（＝\(\hat{\beta}\) は BLUE）。

なぜなら、新たな誤差項 \(u_{t}\) は (i) \(E[u_{t}]=0\), (ii) \( \mathrm{Var}(u_{t}) = \sigma^{2} \) で一定, (iii) \( \mathrm{Cov}(u_{i},u_{j}) = 0,\ \forall i\ne j \) を満たし、Gauss-Markov の定理の仮定を全て満たすからです。

なぞなぞのようなシンプルな変形ですが、非常に強力なツールなのです。また、初見だと問題を解けない/自分では思いつかないため、ここで紹介しました。

\(\rho\) が未知の場合

実務的には、\(\rho\) が未知であることが多いため、以下の手順を繰り返して推定します。

1. 初期推定: まず普通の OLS で回帰を行い、残差 \(\hat{e}_{t}\) を求めます。
2. \(\rho\) の推定: 得られた残差を使って、\( \hat{e}_{t}​=\rho \hat{e}_{t−1}​+v_{t}​ \) を回帰し、\(\hat{\rho}\)​ を求めます。
3. データ変換: 求めた \(\hat{\rho}\)​ を使って、変数を変換します。
   • \( y_{t}^{*} = y_{t} - \hat{\rho} y_{t-1} \)
   • \( x_{t}^{*} = x_{t} - \hat{\rho} x_{t-1} \)
4. 変換後の回帰: 変換後の変数を使って \( y_{t}^{∗} ​= \alpha^{*} ​+\beta^{*} x_{t}^{∗} ​+ \varepsilon_{t}​ \) を OLS で推定します。
5. 収束判定: 推定された係数から新しい残差を出し、\(\hat{\rho}\) が変化しなくなるまで手順2〜4を繰り返します。

手順3のデータ変換の箇所は、先ほどの \(\rho\) が既知の場合とよく似ていることに注意してください。

今回は \(\rho\) が未知であるため、\(\rho\) を推定する必要があるというだけで、やっていることの本質は何も変わりません。

• \( y_{t}^{*} = y_{t} - \rho y_{t-1} \) を
• \( x_{t}^{*} = x_{t} - \rho x_{t-1} \) と定数項に OLS 回帰

という目的のために、\(\rho\) を事前に推定するというだけです。

この考え方は FGLS (Feasible Generalized Least Squares) でも使われ、大学院のコア計量経済学の至る所で出てくる共通の考え方なので、知っておくと良いでしょう。

R, Stata での実装

R でコクラン・オーカット法を実行するには、orcutt パッケージを使います。しかし現在、orcutt パッケージはCRANのメインリポジトリから外れているため、コマンドが使えません。

Stata でコクラン・オーカット法を実行するには、praisコマンド（, corc オプション）を使います。

tsset t   // 時系列データとしてStataに認識させる
prais y x, corc

tsset t   // 時系列データとしてStataに認識させる
prais y x, corc

まとめ

最後に、コクラン・オーカット法について簡単にまとめておきます。